NOTE: This article was originally published in February, 2010. I'm republishing it (category: Revival) as a nod to content that drew interest at that time, as I said I would do at the point of reboot. I have not modified the content–it is identical to what it was when it was first published, so statements that are made “in the present” should be interpreted in that context (i.e., the present is “circa 2010”).
So, at work we’re in this recruitment cycle again. This time it’s aggressive, and we’re really after the cream-of-the-cream. Those hard-to-find coding ninjas who generally don’t ever need to approach a recruitment agent, because of course, the second someone sniffs that they’re on the market, they’re wooed with shares and options and Wii’s and iPads and rubdowns. It’s a mad scramble.
The best way to finger these types is through someone you know who’s really good, who knows someone they worked with at some point who blew their socks off. Unfortunately the network method has failed us—sadly it looks like all talent has gone deep underground, or left the country. I’m partial to the latter because quite frankly, the quality of the meat that our corporate designated agent is passing our way has been found wanting … repeatedly.
But before I get ahead of myself—let’s approach this methodically, like we should a new project.
Step 1: Clearly define what we require
Enter the Senior Developer. As expected, this is all too subjective … a quick zoot over to SO confirms our fears and leaves us unsatisfied: it depends. I wish it was as easy as “Spanish male developer” (si señor!).
Being the “main technical peanut” using our PM’s terminology, the responsibility of defining the standard falls on my shoulders. I do subscribe to Joel Spolsky’s “smart and gets things done”, but the definition somehow falls short … it just isn’t complete.
Here's my take on this one:
Senior Developer Quality 1: Professionalism
Now we all know that you can’t distil what makes a senior developer into one simple thing, but this is one of those undeniably big differentiators. Can you do a good job, consistently? If yes, then proceed to next assessment gate.
Senior Developer Quality 2: Intelligence
Where I come from, there seems to be this unspoken rule: “one doesn’t explicitly talk about smarts”. Because of course, smarts is one of those things that if you don’t have, no amount of experience is ever going to improve the situation. Let’s square up to this, for crying out aloud—if you want to be a senior developer you absolutely must be smart. Preferably, very smart.
Senior Developer Quality 3: Passion
Another big differentiator from the unwashed Mort-cast. You gotta wanna learn, all the time, during meals, on the can, driving to work, driving from work, on the treadmill, aside the water cooler and anywhere else you care to mention. Senior developers have technology in their veins, they live it and breathe it. Excitement isn’t derived from the promise of a ticket to the Super 14 final, but rather the appearance of a postal collection note for that 200MB/s write-rate SSD from Newegg.
Senior Developer Quality 4: Humility
Getting to the point of truly grokking that no matter how good you think you are, there’s always someone else out there who’s better than you are is a watershed moment. In all honesty though, no-one enjoys an arrogant git … it just isn’t conducive to greasing the cogs of the team dynamic. The more numerous the alpha-geeks in a team, the more critical the quality of humility becomes.
Senior Developer Quality 5: Experience
There’s a bit of cross-over here with quality 1, so let’s say that in this case we’re particularly interested in the sort of experience that gives you that technical “gut feel”. After a number of years, the neural pathways have been set up so that you can generally “smell” whether something sounds right or it doesn’t (when interacting with colleagues), and your hunch about where problems may lie tend to be more often right than wrong.
Step 2: Screen ‘em
When it comes to finding good people, and when you don’t have the luxury of a network-enabled direct route, it boils down to a numbers game.
Spolsky advocates the phone screen, but we’ve opted for a technical assessment. Do we really want to waste our time sitting down to chat with someone if they don’t make the bar? So to be sure, this is an effort to weed out those who think they represent our definition of Senior Developer, but who don’t.
A simple test should suffice. I drafted one this morning, and I’m going to publish one of the questions (with sample answer). Now you’ll notice that the problem posed isn’t very challenging (although some of my colleagues beg to differ), but you’d be surprised at how many people who sell themselves as senior developers who can’t do it.
My lazy side originally opted to go for one of those shrink-wrapped multiple choice online assessments ala Brainbench. I’m not going to mention the brand of assessment that is our corporate standard because I have nothing good to say about it—typographical errors, and code that wouldn’t compile in almost every single question? I wasn’t impressed either. Suffice it to say, it’s not Brainbench. Whatever the choice of assessor though, all of these tests suffer from the same problem; they tend to test stuff that we would naturally expect to Google these days. I don’t rate that as being particularly useful at all.
Solver
The plot below shows two functions intersecting over the interval 0 to 4. The two functions are:
y = x² − 3and...
y = x·ln(x)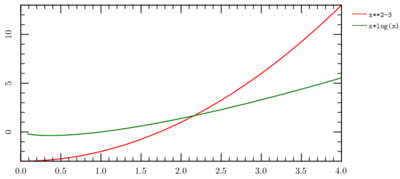
Write a program to calculate the root in the above interval, that is: the X coordinate of the point where the two functions have the same Y value.
Solver, above, may seem overly mathematical and unrepresentative of typical “throw-stuff-in-a-database-and-pull-it-out-again” business requirements, but what it does do is very quickly highlight the sort of person we don’t want.
- Do we want someone who can’t understand the question because it contains “nasty unknowable symbols”? Even if you didn’t do maths at university, surely you did algebra at school? That’s all you need to know.
- Do we want someone who can’t do research on the Internet? Jeepers, I even provided the exact Wikipedia search. The corresponding article, predictably, contains pseudo-code for various algorithms—would you honestly need more than that?
- Do we want someone who can’t be stretched to understanding an iterative algorithm to which they haven’t previously been introduced?
- Do we want someone who doesn’t know enough to fire up the browser and at least try “+”root-finding” +C#” on Google? (Yes, I do check the browser history afterwards :) Of course I’m not expecting Newton’s method here, simple bisection will suffice. Even if our prospective senior has never attended a calculus class, I would expect her to be able to fathom this one unassisted.
Here’s my bisection code, written up and tested in 20 minutes—too much time, I might add, for what I would consider a senior who lives and breathes code:
class Program { static void Main(string[] args) { var lhs = (Func<double,double>) (x => x * x - 3); var rhs = (Func<double, double>)(x => x * Math.Log(x)); var diff = (Func<double,double>) (x => rhs(x) - lhs(x)); const double threshold = 1e-5; Func<double,double,double> findRoot = null; findRoot = ((l, r) => { if (Math.Abs(l-r) < threshold) return l; var mid = (r+l) / 2; return (Math.Sign(diff(l)) == Math.Sign(diff(mid))) ? findRoot(mid, r) : findRoot(l, mid); }); Console.WriteLine(Math.Round(findRoot(1,50), 2)); Console.ReadLine(); } }
Now the big problem with bisection, of course, is local minima, but that is a non-issue because I even provide a graph illustrating that there aren’t any local minima.
It’s time to wrap this post up, and defer description of the how testing against qualities 1 to 5 should be done to another one. Today we presented our first senior candidate with Solver, but you can probably guess what the outcome was when I tell you that he couldn’t nail Fibonacci which was to print out the first 30 terms of the sequence of the same name.

Comments !